Triangle Dimension Formula
How To Find The Dimensions Of A Triangle Sandberg Casonctin B = √ (c² a²) for hypotenuse c missing, the formula is: c = √ (a² b²) 🙋 our pythagorean theorem calculator will help you if you have any doubts at this point. 2. given an angle and the hypotenuse. apply the law of sines or trigonometry to find the right triangle side lengths: a = c × sin (α) or a = c × cos (β). The sum of the lengths of any two sides of a triangle is always larger than the length of the third side pythagorean theorem: the pythagorean theorem is a theorem specific to right triangles. for any right triangle, the square of the length of the hypotenuse equals the sum of the squares of the lengths of the two other sides.
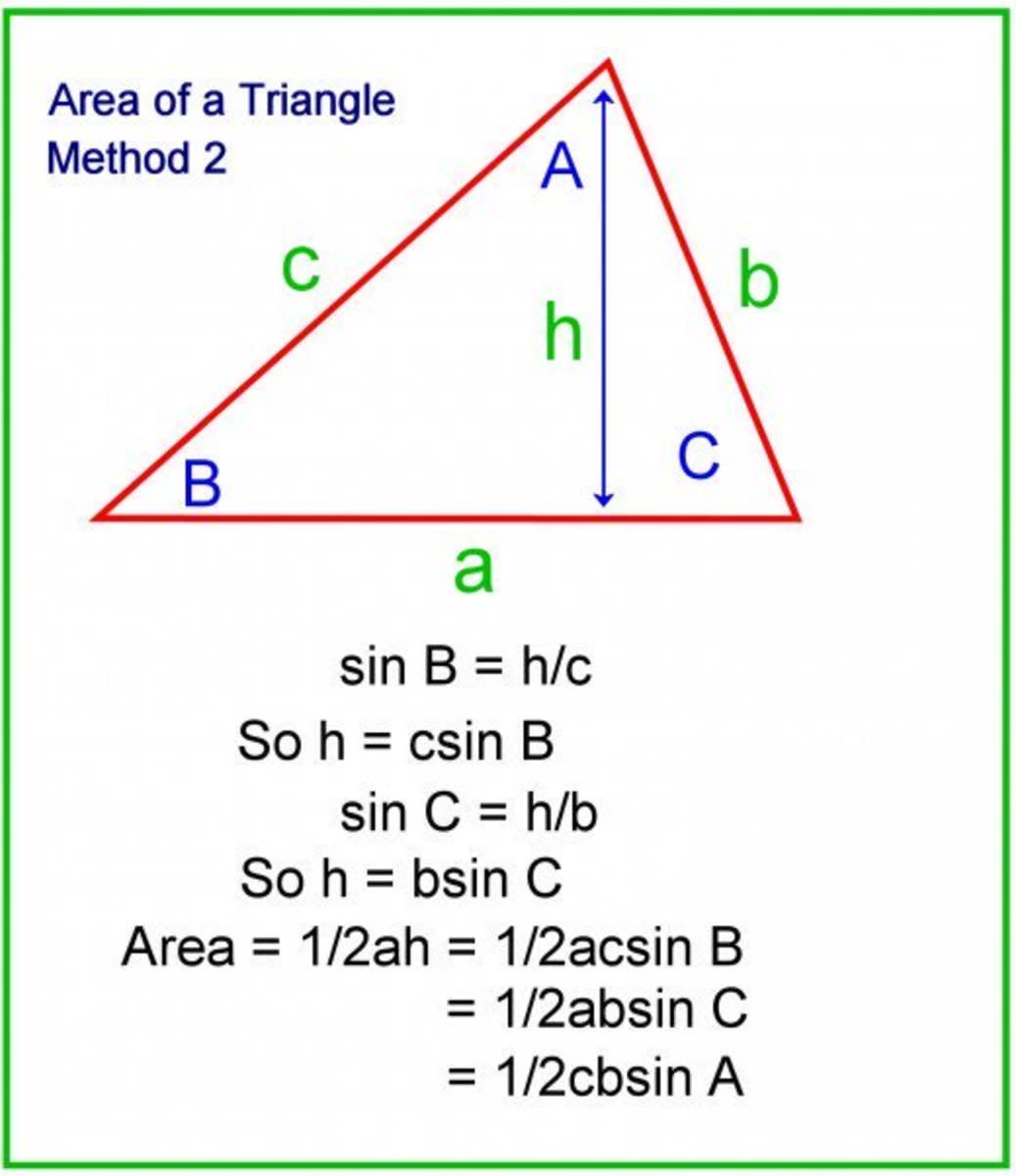
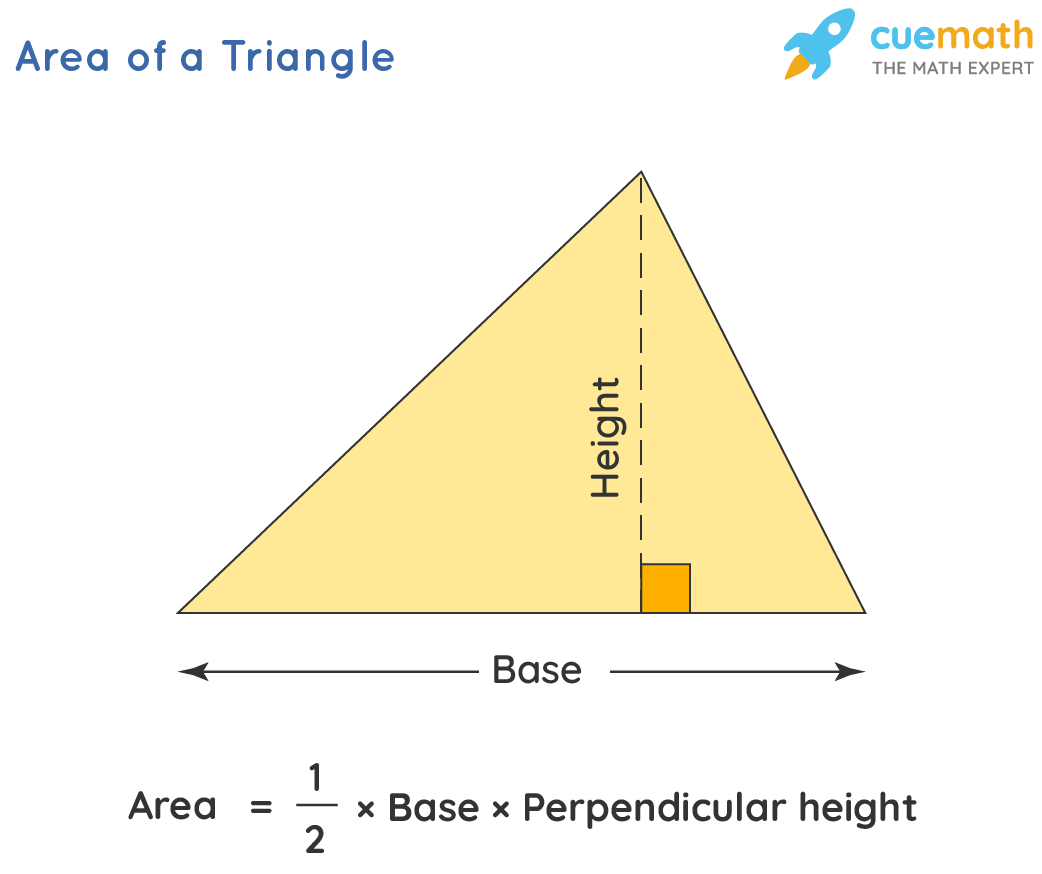
How To Calculate The Sides And Angles Of Triangles Using Pythagoras The 45° 45° 90° triangle, also referred to as an isosceles right triangle, since it has two sides of equal lengths, is a right triangle in which the sides corresponding to the angles, 45° 45° 90°, follow a ratio of 1:1:√ 2. like the 30° 60° 90° triangle, knowing one side length allows you to determine the lengths of the other sides. The base of a triangle = 40 units (given) height of triangle = 25 units (given) using triangle formulas, area of triangle, a = ½ × base × height. = ½ × 40 × 25. = 500 square units. answer: the area of the triangle is 500 square units. example 2: a triangle has sides a = 5 units, b = 10 units, and c = 6 units. To find the angle of the triangle opposite one of its sides, say side "a": square the first side, a. add the square of the second side, b to it. subtract the square of the third side, c from the sum. divide the difference by the length of second side. divide the quotient by the length of first side. divide the quotient by 2. The so called "45 45 90" triangle is probably the most special among all the special right triangles. this is a right angled triangle that is also an isosceles triangle. both its catheti are of the same length (isosceles), and it also has the peculiarity that the non right angles are exactly half the size of the right angle that gives the name.

Comments are closed.